
そんなわけあるかな?
誕生日のパラドックス
突然ですが、自分と同じ誕生日の人に出会ったことはありますか? そんなに何人もいないという人がほとんどですよね。なのに、この記事のタイトルを読んで、ちょっと信じられないかもしれません。
実はこれ、確率論の世界では「誕生日のパラドックス」として知られている現象です。もしクラスメイトが30人いた場合、その中に同じ誕生日の人がいる確率は直感的にどのくらいだと思いますか?
「ほとんどあり得ないんじゃないかな? 1年は365日もあるし」と思うかもしれません。しかし、この確率は70%以上になるのです。なぜこんな結果が出るのでしょうか。不思議なこの現象、その秘密を探ってみましょう。
誕生日と確率の不思議
まず、クラスに30人いるとしましょう。そして、1年は365日ですよね。直感的には、365日もあるのだから、同じ誕生日の人がいる確率はとても低そうに感じるかもしれません。しかし、この「誕生日のパラドックス」の面白いところは、この確率が意外に高くなる点にあります。
その理由は、「人数が増えると、比べる組み合わせがどんどん増える」からです。
たとえば、クラスに2人しかいなかった場合、この2人が同じ誕生日になる確率は非常に低いです。しかし、人数が30人に増えると、その中の誰かと自分の誕生日が一致する確率がぐっと高くなります。
ここで大事なポイントは、「クラス全員の誕生日が重ならない確率」を考えることです。一人ひとりの誕生日が全く重ならないような場合を計算し、それを全体から引き算すると、結果的に誰かと同じ誕生日の人がいる確率が求められます。
確率を簡単に考える方法
具体的な計算は少し複雑ですが、こう考えると分かりやすいです。
- 1人目の誕生日はどの日でも構いません。
- 2人目の誕生日が1人目と違う確率は364/365です。
- 3人目の誕生日が最初の2人と違う確率は363/365です。
これを30人分繰り返していきます。30人目の誕生日が全員と違う確率は337/365です。これらをすべて掛け合わせると、30人全員の誕生日が異なる確率は約0.2937、つまり29.37%になります。
これを1から引くと、少なくとも1組、同じ誕生日のペアがいる確率は約0.7063、つまり70.63%です。このように計算すると、30人という少人数でも確率が70%を超えることがわかります。
「え、ちょっと待って」と思ったあなたへ
ここまで読んで、「え、ちょっと待って。何かおかしくない?」と思ったあなたは、名探偵の素質があります。さあ、気づきましたか? じつはこの記事のタイトルには、少し誤解を生む表現が含まれているのです。
というのも、70%以上というのは、「クラス全体の中で、誰かと誰かの誕生日が一致する確率」を指しています。しかし、それがあなたとは限りません。つまり「自分と誰かが同じ誕生日である確率」となると、まったく別の話なのです。
では、今度は「自分と同じ誕生日の人が30人のクラスの中にいる確率」を計算してみましょう。自分以外の29人のクラスメイトがそれぞれ自分と違う誕生日を持つ確率はこうなります。

これを計算すると、約0.921(92.1%)になります。つまり、反対の事象、「自分と誰かが同じ誕生日である確率」はというと・・・
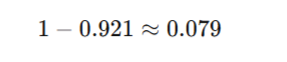
結果は約8%。先ほどの70%とは大きな違いがありますよね。な~んだ、とも思いますし、まだ高いんじゃないかなという気もしてきます(疑心暗鬼)。でも、これが正解です。
確率が語る身近な不思議
この「誕生日のパラドックス」の結果は、多くの人にとって驚きです。普段は意識しない「確率」の考え方が、こんな身近な話題で活用できるとは興味深いものです。
ぜひ家族や友人にも、「30人のクラスで、同じ誕生日の人がいる確率は70%以上になるらしい」と話してみてください。そして、この話には続きがあることも教えてあげてください。「それが自分である確率は約8%」だという、このもう一つの事実も、不思議で魅力的な確率の世界を物語っています。




